OK…I’m horribly stuck on pages 5 through 9.
I simply cannot make complete tangible sense of what he’s outlining.
I completely understand the ratio fractions from the Pythagorean formation that he’s using, but I cannot make any sense of the relationship that he’s trying to show me in this segment. I tried moving past it in hopes that it would eventually make sense given further details, but that didn’t happen. Instead, it just left me feeling like I wasn’t getting things fully given that I didn’t properly digest this segment, so I went back and re-read it three days in a row repeatedly and I still have no fucking clue what the hell he’s trying to communicate.
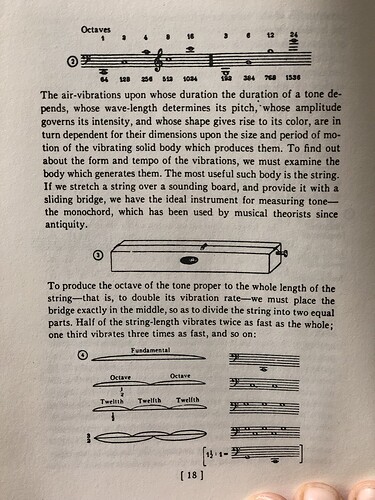
The series of digits being infinite, we have to limit it arbitrarily. The limiting number we call index. For our purpose the index 16 is sufficient. Proceeding, then, to divide the string successively by the numbers 2 to 16, we obtain the following series:
1/1 ( C), 1/2 (C2), 1/3 (G2), 1/4 (C2), 1/5 (E2), 1/6 (G2), 1/7 (Bb2), 1/8 (C3), 1/9 (D3), 1/10 (E3), 1/11 (F#3), 1/12 (G3), 1/13 (Ab3), 1/14 (Bb3), 1/15 (B3), 1/16 (C4)
This part I’m fine with.
…
We write a series on graph paper, in one line from the left to right, using one square (inch or centimeter) for each tone, and next proceed to multiply the string by the same series of digits.
No clue what he means by this. I understand the words, but the meaning is about as evasive as if you just told me that “we are energy, so harmony is found in resonant oneness”.
Now of course we cannot actually multiply the string, but we can imitate the results by using a little trick. That trick is made available through the special quality of one of the intervals we have found, namely, the octave. The octave of a tone, although being a different tone, is a sort of identity, so much so that indeed we call it by the same name. Hence tone relations may be transposed by octaves. Consequently we may begin our multiplication with 1/16 instead of 1/1, simply indicating the octave signatures of the notes we would obtain if we started with 1/1. The experimental series will thus run: 1/16, 2/16…16/16; the intended series: 1/1, 2/1…16/1.
I have, again, no clue what he’s driving at here. I don’t see how the octave is helping here. We’re just running the series forward and backwards numerically.
Given that I understand his nomenclature to mean that 1/1 ( C) is where we start and that 1/2 (C1) is an octave from 1/1, then 1/16 (C4) would be multiple octaves up, not one.
This is a problem I have with him, in general. He’s not clear on his terms, definitions, nor nomenclature. He just whips out the series (for example) without bothering to explain what the hell his shorthand means, and then builds off of that series as if the meaning of the shorthand was understood, without taking any steps to assure that the reader is following along properly with his train of thought and the way he thinks in his personal world.
Anyway…we move on with him running the opposing series, which he arbitrarily calls the “intended series”, again with no explanation as to what the hell that means. Because to me, if you arbitrarily call one series the “experimental” and the other the “intended”, then I’m going to understand you to mean that the first exists purely for the purposes of getting the second, and that the first is not of interest, nor will be used. However, that’s not what he’s doing. So I have no clue what the hell he’s meaning here.
I’m assuming that the “intended” is basically the “negative” series and the experimental is the “positive series”, but he doesn’t use these words because these are clarifications made after him by others.
Anyway…
The result is the following series:
1/1 ( C), 2/1 (C1), 3/1 (F3), 4/1 (C2), 5/1 (Ab3), 6/1 (F3), 7/1 (D3), 8/1 (C3), 9/1 (Bb4), 10/1 (Ab4), 11/1 (Gb4), 12/1 (F4), 13/1 (E4), 14/1 (D4), 15/1 (Db4), 16/1(C4)
Now, this is where I seriously begin to doubt my understanding, because we’re going backwards from the first series (“experimental”), but we’re still increasing what I understood to be the octave nomenclature identifier (the number after the lettering).
The reason I have a major confusion over this is if I follow this logic using wavelength (which is equivalent to a string length for these purposes), then if I run the “experimental” series, we’re fine.
We start at 2109.89 cm wavelength for C0 and end on 131.8~ for C4 and arrive at the same notes along the way in the sequence, and in the right octave for the nomenclature supplied.
HOWEVER
If I then apply this same logic to the “intended” series, I get an ENTIRELY different result.
If I start at 2109.89 cm, I will get the exact same series of notes from the “intended” series as I would from the “experimental” series.
If I start at the other end of the spectrum and start at 8.24 cm, then I will also get the same series as the “experimental”.
But Levy writes out the following note sequence instead as his result:
C, C1, F2, C2, Ab3, F3, D3, C3, Bb4, Ab4, Gb4, F4, E4, D4, Db4, C4
Whereas if you follow the fraction sequence, which ultimately just ends up being a multiplication by the first number because 2/1 is … 2, etc…
Then you get:
C, C1, G2, C2, E2, G2, Bb2, C3, D3, E3, F#3, G3, Ab3, Bb3, B3, C4
Take 2109.89 as your starting wavelength, put that into excel and follow the below:
|Fraction||Decimal|Wavelength|
|---|---|---|---|
|01|01|01|2109.89|
|02|01|02|4219.78|
|03|01|03|6329.67|
|04|01|04|8439.56|
|05|01|05|10549.45|
|06|01|06|12659.34|
|07|01|07|14769.23|
|08|01|08|16879.12|
|09|01|09|18989.01|
|10|01|10|21098.9|
|11|01|11|23208.79|
|12|01|12|25318.68|
|13|01|13|27428.57|
|14|01|14|29538.46|
|15|01|15|31648.35|
|16|01|16|33758.24|
What you’ll get is this:
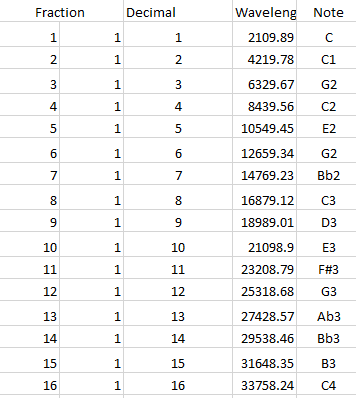
If you take that and convert those ridiculous wavelengths back out, then you’ll get the same run as the “experimental” and not the “intended” series.
(note: I’ve renumbered the octaves to follow Levy’s seemingly “relative” approach to applying octave nomenclature…see comments below about this.)
So I’m entirely lost as to how the “intended” series is supposed to be used.
That’s not even counting that the number sequence for octaves is even more confusing because we’re still going UP in octave count in the “intended” series, but applying the fractions to length you would be going DOWN in octave…not up.
I can only assume he means these octave numbers, then, to mean “away from”, not directionally relevant - though that’s not stated so I have no real knowledge of his intended meaning here.
You can even make this easier by using Hz and reversing the operation.
Instead of multiplying the original starting value (2109.89) by the next fraction (2/1) to get the next (4219.78) wavelength, you can divide the original starting value in hertz (16.35) by the next fraction (2/1) to get the next Hz frequency (8.175).
This gives you the same result as the waveform, but in hertz, which is easier to check since most resources don’t go about listing notes in wavelengths, and most often the ones that do require you to also set a parameter for the air density in question (FYI, when attempting to run vanilla, use Air as the medium at around 20 degrees Celsius - that’ll give you “lab” conditions…more or less).
So this whole section immediately starts to make less and less sense to me the more I try to make sense of it.
That’s to say nothing of the diagram on page 8, which…honestly. I haven’t the FAINTEST idea what the hell he’s attempting to show in meaning with that diagram.

So, yeah…any help you can offer me in understanding what the hell this section is actually attempting to convey, or where I’ve gone horribly wrong would be MUCH appreciated!
Cheers,
Jayson