Composition and Theory

#41

Lol power chords but with synths

#42

Basically…yes. :stuck_out_tongue:
Usually root and octave each on a channel using the same synth and tailored to mid and high frequency shaping. Usually square or saw.
Then a different synth for the 5th. Either square, saw, or sine dependinh on need.
And the minor/major voicing by a pad or choir.
Bass as whatever’s needed - usually closely similar to the root.

And then the melody doing whatever’s poppy and catchy.

I mean…my origin is punk rock garage bands after all. :slight_smile:

My more complex flavors are still just more decorated variations of this. Sometimes I deviate way off and do crazy stuff, but not usually. Usually I write orchestrated poppy punk rock styled into dance music.

Cheers,
Jayson

#43

That’s quite a genre!:ghost:

#44


:stuck_out_tongue:

Cheers,
Jayson

#45

Yeah so I’m only two chapters in and I have just been playing around for five minutes with a few ideas. It definitely unlocks a whole other world of harmony and it totally works too. Really worth the 30 bucks so far.

#46

I’ve been reading it a bit.

Communication is not this guy’s forte. He goes through a lot to explain a little.

What I’ve got so far in my translating an understanding.

-1, -3, -5, -7, -9, -11, -13, -15, -17, -19, -21, -23

These are your intervals.
Pick a key.
Place your key note in the 4th from the end position (-17).

Line up chromatically from there rolling forward until you wrap back around.

Say, Ab.
Ab, A, Bb, B, C, Db, D, Eb, E, F, Gb, G

But lined up it becomes
C, Db, D, Eb, E, F, Gb, G, Ab, A, Bb, B

Then you just count the interval for that position to get the counter note a bit more easily than the author’s way of explaining.

Haven’t read it all yet, obviously.

Cheers,
Jayson

#47

I’ve started building an excel file to do the calculating.
Got the core done so that you put in the key and get back the table array.

Just needs the ability to support selecting chords and spitting out their counter part.

Cheers,
Jayson

#48

Yeah, I end up skimming a lot of shit (which I don’t like) so i keep having to reread things to fully grasp what he is saying.

As far as the rest of your analysis… I don’t follow…

Here is how I take it (and just work with me for the sake of the idea)

A Cmaj chord and an Fmin chord are the same chord but in opposite directions.

so following along… start at C3 (middle piano) and go up 7 half steps to G (5th) then go up 9 more half steps to E (3rd), then 8 more half steps to C5

Now do the same thing but in the opposite direction starting on C3, so 7 half steps down to F, 9 more half steps down to Ab, and 8 more half steps down to C1

So how I take this is that everything revolving around the root of your scale (or the target)

For an example I wrote this to share what I think I have found

So the first 4 bars goes

I - IImin - I6 - V7

The second 4 bars repeats

I - IImin - I6 - (V7)

I replaced the V7 from the first 4 bars with something that MOVES exactly the SAME… but I set up the notes of the (V7) to move in the exact amount of steps BUT in the opposite direction compared to the original resolving V7 chord. I think it works perfectly and adds a bit more color.

The third 4 bars is the same as the first except I voiced or arranged the notes of the V7 chord for smoother voice leading, as you will see why but here it is

I - IImin - I6 - V7

The fourth set of 4 bars goes

(I) - IImin - I6 - (V7)

The Cmaj chord or the I chord was replaced with its “negative” counterpart Fmin, and I think it definitely has applications in writing for sure, that chromatic line of G - Ab - A which is produced sounds very pleasing to me and interesting, then I use the replacement “V7” for the final resolution back to I or Cmaj

tell me what you think

#49

It’s computationally simple and drop brain-dead easy to remember the pattern.
However, this approach isn’t easy to use because it’s ridiculous to count -23 intervals sitting at a piano.

It’s just that it’s really easy to plug this into a computer using this pattern.

Take C; not the scale. Just starting from C chromatically.

|C| Db D Eb E F Gb G Ab A Bb B

Now we rearrange the lineup so that it fits for the pattern sequence.
E F Gb G Ab A Bb B |C| Db D Eb

Now we add the pattern sequence under that.

  E	  F	 Gb	  G	 Ab	  A	 Bb	  B	 |C| Db	  D	 Eb
-01	-03	-05	-07	-09	-11	-13	-15	-17	-19	-21	-23

Now we just take the exact interval (keeping in mind it’s subtraction) from the note above and apply it below.

  E	  F	 Gb	  G	 Ab	  A	 Bb	  B	 |C| Db	  D	 Eb
-01	-03	-05	-07	-09	-11	-13	-15	-17	-19	-21	-23
 Eb	  D	 Db	  C	  B	 Bb	  A	 Ab	 |G| Gb	  F	  E

This doesn’t give you the SCALE.
It just gives you the full length inversion of whatever you have above it in a very drop dead easy pattern sequence.

If you want a REALLY easy human way, then you take the exact interval pattern of the SCALE, for example, C Major starting on C and running 2, 2, 1, 2, 2, 2, then you start at the 5th, G, and go DOWN in exactly the same interval sequence. Which will generate G Phrygian (G, Ab, Bb, C, D, Eb, F).

Cheers,
Jayson

#50

Aaaand BOOM!

Updated my CAT (composition assistant tool) to automatically spit out the negative theory scale when you pick a scale.

Now all that’s left (haha…“all”…it’s a pretty big chore) is to build the negative chord support.

Check it out.

Cheers,
Jayson

#51

But i think this is more than just a scale… I had a completely different interpretation than you did. Maybe I am not following what you are trying to achieve exactly. did my interpretation make sense?

and yes… If you take the

C locrian scale, flip the pattern and run it you get C lydian
C phrygian scale, flip the pattern and run it you get C Ionian
C aeolian scale, flip the pattern and run it you get C mixolydian
and If you take C dorian pattern and flip it… well you get C dorian again

But that isn’t the point of the book i don’t think

what did you think of my analisis

#52

Oh yeah, it’s on point.

And negative harmony isn’t just scale, it’s also about switching out chords in a progression.
Which, that part will be more supported when I update CAT to deliver negative chords.

For the time-being, until I get some more time to tinker, it delivers the negative scale result so that at least you know what notes are the negative version of what you’ve picked as your scale.

What I was more answering to was that the explanations of how to generate a negative scale given any positive scale (at least, that I’ve read or seen) are pretty much…terrible.
It all relies on overly complicated dives into degrees and major/minor nths etc… which just generally causes novices to scratch their heads and not understand what’s going on - what’s the most basic fundamental pattern at play.

Negative theory, at its most basic, should take all of a minute or two to describe - honestly.
It’s not super complicated to describe the basic fundamental and deliver something that is usable by even a 5th grader with some lessons in piano under their belt, but the explanations I’ve seen have been overkill and convoluted.

Cheers,
Jayson

#53

Okay, cause I’m seeing like the tone C has 2 triads

C maj and F min

This goes for any tone

The note C also has two “V7” chords that act the same way and resolve the same way but in opposite directions

Idk that’s all I got

It’s all about relation to specific notes.

This is a whole other way to view harmony and music

Like he said C min isn’t a variation of C maj. To me it’s part of G maj

#54

Like C min should really be called G dark and G major called G bright

#55

You lost me a bit there.
C has effectively 7 triads because you have C, Dm, Em, F, G, Am, Bdim since the “chords of C major” are just start on a note, add the 3rd, and then the 5th from your starting note, and start your note progressively C, then D, then E, etc… along the scale.

Did you mean tonic triad?

Edit: oh! Are you counting the Fmin from the G of the C major overlapping to the C of the G Phrygian and counting that C then as the root, counting up from there a 3rd to Ab and then a 5th to F?
And then reforming that so that F becomes the root of the chord instead of C, making it an Fmin?

To me, the tonic triad you get back is Gm since the correlated scale is G Phrygian, which gives G, Bb, D as the tonic triad.

Cheers,
Jayson

#56

I think we are getting close… let’s throw all the scale out the window for a minute.

So the tone C physically in nature produces overtones that will spell out a what we call C major chord (plus a few extra notes but not important as the first tones)

You flip that exact grid and it will spell out a what we call F minor chord. It doesn’t happen in nature.

Onother way to look at it is the same way he does in the book… he divides a string in rations (much like the workings of a guitar or violin) producing the notes of a so called C major chord.

If you flip those ratios you begin to make the string longer, and those same ratios that created a C major chord will now produce a so called F minor chord when they are flipped.

#57

I’m not seeing that.

If I have the C, yeah, it will inherently spell out a C Major Chord inside of it.
That grid looks like this (focusing on only the highlighted notes).

image
image.png770x23 1.24 KB

If I flip that grid around, using the negative theory method, then I get.

image
image.png771x23 1.33 KB

Or do you mean something else by “flip that exact grid”?

I can kind of see what you are thinking if we’re on a Tonnetz grid, start on a C major chord
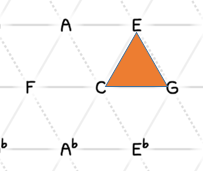
image

, flip to its negative chord (Gsusb6…pedantically, or you can reshape that to C minor if you hang onto C as the root instead of taking the negative root G, anyway…),
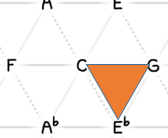
image

and then flip that backwards, then we land on F and move the root to the F instead of the G.
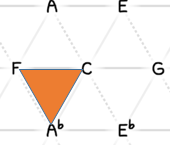
image

Basically always making our root to the left.

Cheers,
Jayson

#58

This is the beginning of what the book talks about.

The point of the book is to look at harmony in a different way. I think that is being over looked greatly.

Are you reading the book or reviewing differ things on the web about the subject?

#59

When I am saying flip the graph I’m talking about the overtone series btw…

#60

Reading the book as well as checking the fad.

Haven’t gotten far on the book yet.

Cheers,
Jayson