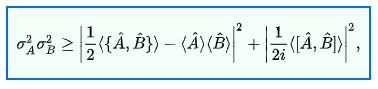@Jayson … thanks for some ideas towards me getting a new hobby…
You probably already know and considered this but in any event…I’ll state it anyway
Also might wanna look towards a planets gravitational pull by calculating its overall mass in order to calculate the radii of the atmosphere…
Or the alternative is to treat a planet like a black hole by measuring it via the way light or asteroids/other objects bend around it if possible
Glad to have helped inspire a science hobby! 
To be clear, I’m not working on atmospheres of planets.
I’m working on astrosphere’s of star systems.
It’s sort of like a star system’s atmosphere…ish.
It’s a “bubble” that forms around an entire star system as a result of the star both spitting out all of those charged particles which eventually hit a termination point, and the motion of the star through space.
It’s usually impossible to observe because it’s way too fine and stars are too far away.
However CW Leonis is so big (700 times the size of our star) and powerful of a star that we can take pictures of its astropause (astropause is the first demark point - going out from the star - of the astrosphere…like the stratosphere to the atmosphere).
Here’s what it looks like.
The radius of this astropause is ~84,000 AU.
-ahem-
That’s 84,000 times the average distance of the Earth from the Sun.
To give some perspective. To travel that far at the speed of Voyager 1 (fastest human made spacecraft) which travels at 17 km/s (>38,000 mph), would take over 23,000 Earth years.
At the speed of light (which is the speed photons are ripping off from this star) it takes just under 16 months.
And this (mixed with how close it is to us) is why you can see this thing’s astrosphere. It’s huge and powerful.
So this is what I work on cataloging.
Cheers,
Jayson
Good luck Jayson. It sounds like a lifetime project. This is something worthy of the mathematical mind of Mr Spock. I was not familiar with the concept of stars having an “atmosphere” but as you say with all the charged particles being emitted there would be such a shell of material. Even our Sun has its “Solar Wind” that impacts the atmosphere on the Earth and we can assume the other planets of our system. Compared to the stars you are studying it is probably “tres centimes”
Indeed!
The astrosphere turns out to be really important.
We’re only now learning to what degrees.
We know now that it blocks a huge amount of interstellar cosmic rays, sooo…that’s kind of important.
So being in the green zone for a planet might not be enough.
It might also need to be in a green zone from its star’s astrosphere so it doesn’t get pounded with interstellar cosmic rays.
Cheers,
Jayson
Actually, this brings up a point that is a big thing for me.
We hear a lot about citizen and amateur science these days, but when you look into it beyond the buzz, what you find is that it comes in the form of image clicking or allowing your computer to be used for shared processing power.
Once in a while it’s an amateur astronomer spotting or tracking something professionals couldn’t because telescope time is rare and expensive.
Most of the time it’s very passive interaction. You’re not usually doing any science as a “citizen scientist” if you join a project.
But there’s one area of science which has a massive hole in it that didn’t use to exist.
Data analysis.
This was once a job which produced a bunch of findings.
The most famous one?
Hubble’s discovery of the universe expanding.
He would not have had this without the computer, Henrietta Swan Leavitt.
Yes. I said computer. Yes, that is a human’s name.
Before our version of computers, computer referred to humans. A job we now call data analysis.
It’s a typically boring and hard job requiring imagination, and diligence…and a lot of patience.
See, today we have data analysts working in science in hordes. However, one very large difference is that today’s analysts belong to a specific project in most cases because of how technical and refined science is today. Further, the data of a project is usually isolated from most of the community outside of the data relevant to the study itself.
All the extra data collected is just sitting in computer or cloud storage in massive volumes and only gets used when someone processes it with software which has been programmed to answer a specific query.
See where I’m going?
Flip back to Hubble’s time.
Leavitt didn’t work for Hubble. She died before he used her finding.
She found what we now call the standard candle.
Her job was for Harvard as a whole; not one project.
Her task was to take plates from observations by astronomers and catalog their brightnesses (among other tasks).
It was when she was doing this task for Harvard in general that she started to notice a relationship in the brightness which wasn’t part of her original task (which was cataloging variable star brightness).
This eventually lead to “Hubble’s constant”.
She realized this because she would take plates and lay them on top of each other (glass) to determine the changes in brightness over time. Some…didn’t.
She went on to work out much of the meaning and how to go about using the data through further analysis.
The point here is no software today would do this behavior.
If a team has a massive pile of data and sets to analyzing it, the software will only do what it’s asked to do.
It wouldn’t care about things off to the side that are curious patterns.
Further, again, the data is isolated.
Astronomers don’t just have petabytes of all observational data ever just sitting around to endlessly mine.
It’s separated and shelved all over the place.
If there’s not a catalog, then the data isn’t community wide in access.
Data might be made available, indicated in the reference section of papers, in case anyone wants to go play with it.
However, no one has the task of collecting all this data and cataloging it like human computers of the old era.
So not only is no one looking to catalog the data and keep an eye for patterns, no one’s even piling all the data together in the first place.
And this is where I think real citizen science should happen.
A large chunk of this data is publically available either in papers or listed in papers as available data in some online digital storage of the research group.
It just takes folks to just go grab it and compile it!
You only need to know the most basic math and scientific terms and principles to do this work most of the time!
Most of the time, just using excel works fine enough for starting out a catalog (yes, eventually a proper database would be needed).
One day, in a perfect world where I accomplish all dreams, I hope to make a site which allows regular people the ability to go scan through papers and data sources and submit catalogs of data to the site.
That, I think would be a HUGE leap forward as we have thousands of papers flying around a year and no catalog of their data. None!!!
NONE!!
In the meantime, I encourage everyone! Go collect and catalog research data!!
If you need help, call on me. I’ll always help show the way. It’s not actually too hard!
Help save science from its own death by data spam!
Cheers,
Jayson
Yes, Jayson, you make some very good points about finding and compiling data from many and diverse sources. With my aging (and needing replacement) computer, my interest in science has to remain on the periphery as it were. In your case it has become something much more serious and you are to be commended. I was watching a short animated clip recently trying to explain the concept of “Strange Matter” but I think I might have to run it again to get my thought clear on the ideas put forward. This would come more into the area of theoretical physics I would assume and not the area that you are pursuing.
Tinking around today; bringing the atomic data into the Phi method that I’ve developed.
What you’re looking at here is 95 atoms.
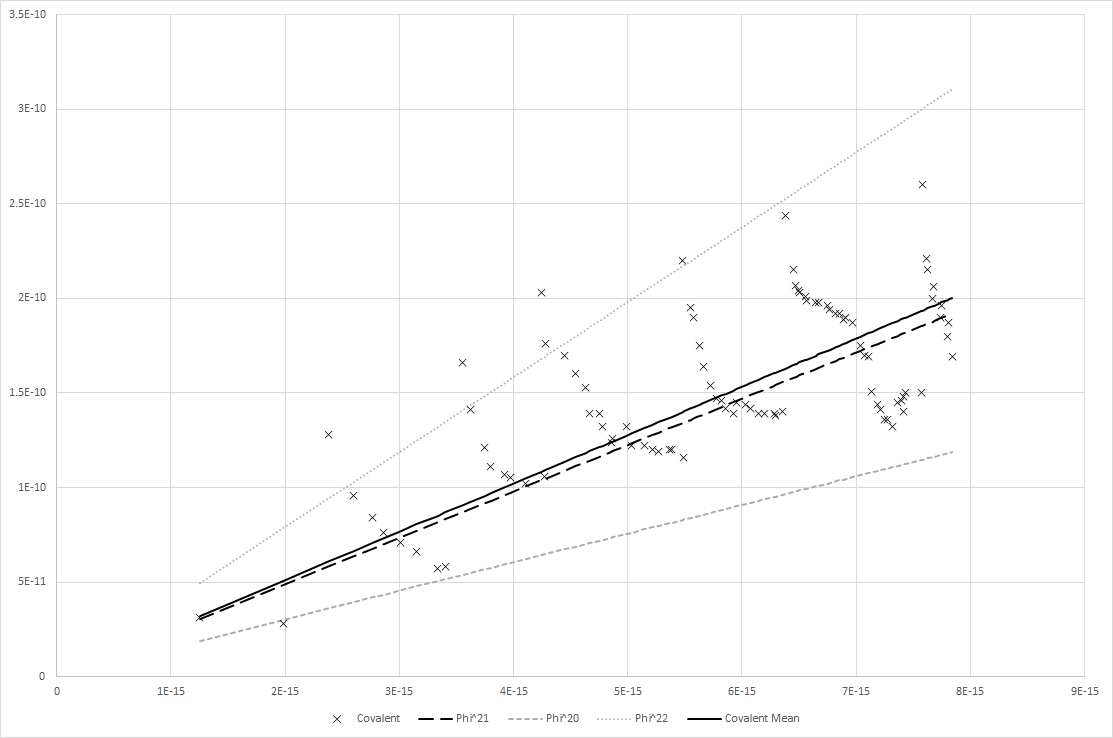
What’s plotted is their Covalent Bond Radii (Y axis) cross sectioned according to their Nuclear Radii (radius of nucleus - X axis).
The X’s are plot points of each actual atom’s real values (or, rather, to be very specific, the cataloged Covalent Bond Radii and the calculated Nuclear Radii given the formula R=r0A^1/3 - the standard formula for determining the radius of the nucleus, where A is the atomic mass, r0 is the radius of nucleons…protons and neutrons…approximately 1.25 to 1.3 fm - read more here if you want https://earthphysicsteaching.homestead.com/Calculation_of_Nuclear_Radius.pdf).
So I have 95 nuclear radii and covalent bond radii.
I then divide the nuclear radii by the covalent bond radii to find what the percent is that the nucleus’ radius is of the covalent bond radius of the same atom.
Think of this like asking what percent the hub radius is of the total wheel radius on a bicycle.
Next, I then take these values and find the mean (that is, the average).
This tells me the average percent a nucleus’ radius will account for of its covalent bond radius.
As an average, it’s going to be wrong if you apply it to a specific sample. Because it’s a sample average.
Anyway, next, I then turn back around and calculate the covalent bond of each atom given the following formula.
Rcov = Rnuc*Phi^21
What this means is that I take a nucleus’ radius and multiply it by Phi (which is calculated by (sqrt(5)+1)/2 … or, 1.618 etc… ) to the power of 21.
So, firstly, Phi to the power of 21. And then multiply the nucleus by this value.
Why Phi^21?
I’ll get to that later.
Anywho.
So, this equation’s results are plotted as the large dashed black line.
Using Phi^22 and Phi^20 are also plotted using different dotted and dashed lines, respectively.
This kind of shows a perspective - a sort of Maximum and Minimum; so that we can see if Phi^21 serves the optimal middle of the road.
What this chart basically shows is that running the atoms across Phi^21 creates an almost identical line to the mean of the relationship between the nuclear and covalent bond radii.
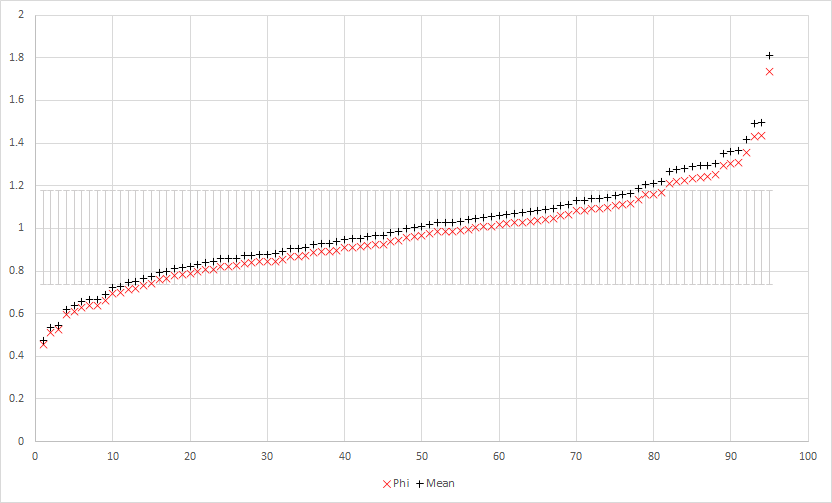
In fact, if you take the mean and apply it back on all samples of the atoms to calculate covalent bond radii, and then take that value and divide it by the real covalent bond radius, you now have the amount of difference by factor that the method of applying the mean produces from the actual value.
Now, if you take the Phi^21 produced covalent bond radii and divide it by the actual covalent bond, you again, have the amount of difference by factor that this method creates from the actual value.
When you compare these two method’s differences by factors per sample against each other, you get this:
The grey bars in the middle around 1 represent one standard deviation.
Meaning, calculating by Phi^21 is effectively equivalent to calculating by the sample mean of the 95 atoms.
In fact, it’s almost impossible to tell the difference.
If you run a Pearson Correlation (i.e. a comparison of the linear correlation between two sample sets of data) between the Mean produced values and the Actual values, you’ll get the result: 0.698802
That means, not very tightly related…which is easily seen when you look at that first graph where you see X plot points all over the place, and the mean (solid black line) right down the middle which doesn’t look very tightly locked in with the shotgun blast of X plots everywhere.
So that makes sense. As noted, the mean from a sample group isn’t going to lock-step with each sample very tightly in many cases. This is why you usually see things like +/- after an average or mean, because there’s a deviation that has to be calculated…in this case, the standard deviation is 9.00289 X 10^-06, which is substantial when you’re mean is 3.91635 X 10^-05.
If I moved that to numbers we’re all more familiar with seeing, then it would be like having the mean equal 100 and the deviation be 23. So almost a quarter of the value in wavering up and down all over the place.
Again, not all that tightly correlated, but that doesn’t much matter. We know this is going to happen because it’s a mean of the sample group.
However, back on track, what is remarkable is this.
When you run the Pearson Correlation between the Phi^21 produced values and the Actual values, you also get the result: 0.698802
In, fact.
You don’t just get 0.698802 on both. You get exactly 0.698801854844335 on both
Which is unreasonably functional. It effectively means that you can determine the mean of the relationship between the radii of the nucleus and covalent bond by nothing more than multiplying the nucleus radius by Phi^21.
This also just happens to be the same value that does the same thing (like, right down to the whole bit about the mean and everything) with Astrosphere radii in comparison to the relationship with the Stars’ radii.
And, it also happens to be the same set R x Phi^0, R x Phi^1, R x Phi^3, … R x Phi^21 (where R is the radius of a star) which generates an exponential line that will average an R^2 value of 0.98 +/- 0.013 of Semimajor Axes of Planets in main sequence star systems (R^2 is a value to determine how well fitting an exponential line is to plotted data - normally used to determine if a trend line is best representing the data … … … semimajor axis is a consolidated mean of a planet’s orbital distance from its star).
In other words…
A source’s radius multiplied by Phi to the power of n (where n is some number from 0 to … so far 21) seems unreasonably good at punching out a rough ballpark region of propagation for some given counterpart to the source.
Imagine, for a moment, if you could take the radius of a tree’s trunk and multiply it by Phi^21 to know the rough radius of its outer-most reach of its branches.
And then imagine that you could do the same thing for the radius of the rings caused by a pebble dropped in water.
That’s the kind of oddity that this is.
Now, it doesn’t do anything. It doesn’t say anything meaningful about physical mechanics. It’s strictly the a numerical analysis and that’s all.
A neat numerical coincidence. A really neat number coincidence, but that’s it. It’s not some mechanical rule of nature.
This was something that I found by accident. Originally, I found the odd relationship between atoms and stars because I wanted a baseline for the astrosphere catalog and a sample size of 21 stars is hardly substantial enough to draw a mean off of and create a baseline from it.
So, I figured, what the hell. I’ll use atoms’ relationship between their nucleus and covalent bond to create the baseline and even though it’ll be off, it’ll be uniformly off and that’ll at least be something.
Then I found, to my surprise, that atoms and the sample of stars I had shared a very similar mean (it was something like 0.0040% to 0.0037% originally).
Then one day, someone in a group asked if anyone thought that Phi had any relationship to the expansion of the universe.
I didn’t think so, but I was reminded of Phi as a value for correlation of proportional relationships of self-symmetry in systems (e.g. phyllotaxis and Phi … deep dive / shallow dive), and so I literally just grabbed the star radius data that I had, flipped on phi, set a series of powers ranging from 0 to some high number and ran the set.
I didn’t expect anything; it was more just a curiosity. When the astrosphere radius kept popping up at Phi^21, that’s when I got interested. When I asked, “Why 21?”, I decided to check the stuff between 21 and 0 … well … the only thing between a star and the astrosphere is mostly … planets. So, I collected a bunch of data on planetary orbits and went about checking and that’s when I found the sympathy with those and this Phi approach.
But until now, I hadn’t bothered to swing around and actually check where it all started; back at the atoms.
And, at this point a bit unsurprising to myself, it holds there just as well.
Anyway…I’m rambling.
Just geeking out on a hobby.
(btw, if you’re reading along and a bit math savvy…yes, the R^2 values are just the Pearson Correlation multiplied by itself.)
Cheers,
Jayson
Right so there are things such as mathematical inequalities, which can be solved/ are held to be true by providing a solution set of real integers for the value of x for the inequality to hold…so what if I were to apply the same concept which I’m guessing has already been thought of…to physics…for some inequalities if im not mistaking can balance out by being (greater than or less than) or equal to an absolute value, for the instances where the value of x is undefined for the inequality to hold maybe we can use a complex number which is a + bi, of which i is being used in (a+b) is being used to quantify the undefinable in order to complete the solution set of certain inequalities… and i can be defined as (i squared = -1)…those are my thoughts based on some of the basics of what I’ve learned so far
Tl:dr maybe inequalities can be used to describe things in physics such as the relationship between dark energy/matter And regular energy/matter or some principles of quantum mechanics or whatever…if I’m wrong or this has been thought of before whatever just a thought I had, at least I have thoughts now…lol
Also what if standard energy, in the form of heat, joules, converting objects with mass…, kinetic, etc… and dark energy can be conceptualized as both being apart of a greater force like how the positive charge and the negative charge are two elements that function as an overall part of the greater force known as electromagnetism…
I’m going only based on the thumbnail and memory here, so I could be wrong. But I believe this video should talk about how the laws of electromagnetism can be derived from quantum field theory, which is one of the things that give quantum field theory so much credence. Quantum field theory also describes nearly all other forces accurately, with gravity being the most major exception that people still need to figure out.
Actually, yes, it is employed quite a bit.
The most famous of these is probably Bell’s inequality.
https://en.wikipedia.org/wiki/Bell’s_theorem#Original_Bell’s_inequality
Although, there is actually a more famous inequality that most folks don’t realize is an inequality: Heisenberg’s uncertainty principle.
Which was originally formalized as:
Or said another way, an inequality.
These days, the principle refers to a wider variety of inequalities that have been designed around this principle (as there are several now that we have so many constituent properties to so many types of quanta).
In fact, it is this employment of the inequality that permitted the ICFO team to effectively “beat” the uncertainty principle well enough for the most refined dual measurements to date.
You can see their paper here.
And you’ll see an inequality equation almost right off.
Don’t get hung up on the = sign being there; that’s just stating the output is reformed as that.
The real work-horse is this first bit.
As you can see it’s similarity to the uncertainty principle from above.
As well, the more generalized formulation of the Robertson relation:
https://en.wikipedia.org/wiki/Uncertainty_principle#Robertson–Schrödinger_uncertainty_relations
Doing something like this is the definition of Unification.
And, for what it’s worth, I don’t think the idea of treating them as part of a whole is off.
The reason that I, personally, don’t, is that, to me, the actual driving ultimate force is pressure.
Everything else, in my mind at least, is derived out from the effects of pressure. It’s just not very functional to derive the pressure all over the place by comparison to just grabbing the specific tool for the job at hand - so to speak.
It’s somewhat like how we know that general relativity is a more correct version of gravity, but most of what we use - even at NASA - is the good old Newtonian equations for calculations.
We only really bother with GR when we need to account for time relationships between two things at very different heights and speeds so that synchronicity doesn’t slip (e.g. GPS).
I view it like this.
Because if you stop and think about interstellar space, what you’re looking at is massive pressure.
Massive enough to push back against the outpouring solar winds blowing off of our Sun and cause it to have some kind of limit to its reach, compared to just going and going and going.
Remember that bit above about CW Leonis?
It’s stellar winds are a billion times more intense than our Solar wind (400 km/s).
And it is even being constrained by the ISM (interstellar medium). All-be-it, at around 84,000 AU later, but still. It’s being constrained.
That is impressive. Especially when you consider that ISM is essentially the background of what is the entire universe and is spread out over everything everywhere.
The shape of the channels of this pressure, somewhat like the shape of channels in ocean currents under water, can change the temperature of a region - just off of the pressure involved.
And that temperature shift makes all the difference between nothing interesting happening, and -POP!- virtual particles tickling away in some novel manner.
If everything in the universe were shut off, except for the ISM, it would be like a very still lake, but a very, very big lake.
Eventually, if you wait around long enough, there’s going to be a difference in one part of that “lake” from another. Just by consequence of the pressure itself being pressure and the expansion itself.
And if you were to add a single particle to this, and (if you could) make it hold itself perfectly still, it would actually eventually end up moving because the ISM itself is moving because it sort of pushes and pulls on itself (like weather maps with pressure systems…which…again, if you think about it, those Earthly pressure systems give rise to temperature and electrical interactions - which, both are electromagnetism).
However, the universe of course doesn’t exist in such a way, and there’s lots of stuff in it, so the various ISM differences (which, there are lots - it’s not universal at all) really get things moving around and make their mark on things.
Velocity and mass of an object go a long way, just like it’s not odd to think of a boat having a good velocity and mass which can overcome a strong current.
My personal opinion is that gravity is a consequence of the ISM pressure of the universe.
I also don’t think that gravity would be found to be the same everywhere in the universe. I think it is remarkably close to being the same - ridiculously hardly different, but the “constant” state of it is minutely different (I think) depending on your ISM.
Sort of like how on Earth we have air density and we don’t think about that, but it’s not actually universal. We treat it like it is in simple equations, but it’s really not the same over the whole planet, and the pressure systems which power the weather radically take effect on what the density of the air is.
The hotter the air, the lower the density. The cooler, the higher. (simplified)
So in Arizona, for example, they have to choose not to fly a plane sometimes because the heat causes the air density to drop (become too loose) to a point that causes the wing’s to not be able to function correctly (wings actually rely on displacing air particles…which is a bit hard to do if air particles are not well packed together…it’s like having 100 people to hold up a stage and move it around, and suddenly having 10 people. Not going to work).
I believe gravity is likely the same. The pressure of the ISM moves differently in different regions of space (we know this already), which I believe if it were to be much different in some region of space, then we would find the reaction by matter in that region to that pressure to be different than we experience in our local bubble.
Quantifying all of this into a single unified equation, however…oooph!
THAT would be one damn hell of a task! 0.0
Cheers,
Jayson
@Jayson
Not sure if you know of Srinivasa ramanujan and apparently before he died he had a few notebooks full of equations
Not sure if you knew but thought I’d share anyways because math and physics sort of go hand in hand…so… will do some further digging and go into that rabbit hole once I cover the basics of calculus and physics…
Lol An equation for everything would probably consist of the ever changing distortion of the various dimensions of space time being modified by a self sustaining feedback loop that quantifies entropic cycles…
The entropic cycles im guessing are defined by a form of kinetics of which the process is similar to how water evaporates from the ocean which is in a dynamic state only to become rain and return to the ocean…or conversely how water freezes turning to ice or snow and then melts to become water or water vapor…with the distribution of energy constantly shifting back and forth creating a weird cycle
I’m totally making that up though…I really haven’t the faintest clue lol
As your friend i gotta say you guys are just getting in over your heads here with the charts n graphs it’s allll meta maaaaaaaan
The problem with the physical sciences today is that they are bordering on the metaphysical, and you start to wonder if you are reading a scientific or a mystical treatise. Are we knocking on the door of God’s abode?
I know of him, but not much beyond that. Just that he existed and is another example of a great mathematician.
Eh.
It depends.
If you’re talking about physical science in labs, then we’re doing remarkably well. We’re able to measure and quantify events the early 20th century’s greatest minds could never imagine.
Dirac would be beside himself at the work of the ICFO team.
LIGO would baffle all of the greats of physics history - that thing is remarkable!
If, on the other hand, we speak of physical sciences in terms of including theoretical cosmology, it gets a little less concrete, and if we go a step further into theoretical quantum physics, it becomes even less stable (especially in the media and “science communicators”…sheesh, they mess this crap up constantly…e.g. “a particle doesn’t exist until observed” -cringe- Dirac and Heisenberg rolls in their graves).
If you want the most obscenely non-concrete of them all, then look no further than the arena of Grand Unified Theory. Oooph! This stadium is filled with nearly religious woowoo, such like M-Theory or String Theory - things that aren’t even falsifiable, and not only not falsifiable, we know for a fact that we won’t ever have the ability to falsify them one way or the other (because, for example, they require a particle accelerator the size of the solar system…lol…yeah, OK).
On the whole, though, where it really matters, things aren’t as bad and silly as it looks in the public presentation of this stuff.
It’s just the attempts to grab the public’s attention often has lead to some incredible silly hyperbolic designs in the expression.
That’s actually why, in another thread, I suggested Quantum: The Great Debate (short name) to @bfk - because it does a great job of walking the reader through the historical building of quantum physics, which entirely gives a different mindset than attempting to approach the subject from today’s zeitgeist to make any sort of sense of it.
Cheers,
Jayson
On another tangent…
Well, here it goes!
https://app.code4socialgood.org/project/view/2112
This is my attempt to get this project going. I’ve one fish biting; we’ll see if any other volunteers sign up.
You can jump to the whitepaper here
Cheers,
Jayson
Well I was able to find his last notes for free on pdf via quick Google search it literally was just
ramanujans lost notebook part x free pdf download
so…I downloaded it to my phone for interesting intellectual material to look at during my free time instead of watching a YouTube meme/vine bullshit which makes people into zombies
@Jayson Once I learn enough, I’ll probably dedicate my efforts to coming up with the necessary maths needed for asteroid defense, even though I’m not that smart…nor do I have the connections, I think that asteroid defense is something worth pursuing so…cause holy shit that shit is scary to think about… and I’d rather not be an ostrich sticking my head in the sand if you know what I mean…so
I think the math we have already would suffice.
The way I see it, the main hindrance of building a fleet of space ships and space stations, capable of actually doing anything helpful about potential threats from space, is political in nature
The energy and money needed for building anything with sufficient defensive/deflective ability out there is simply beyond the scope and will of Earth’s current political leaders.
But, as far as I can tell, it would be possible (although enormously expensive) to create a functional defense-system with the knowledge and technologies we already have at our disposal.
The problem of turning our culture away from personal greed and habitual shortsightedness, - is not a mathematical problem.
My theory for everything
Yes it is a joke
Expanded to include probabilities and heisenberg uncertainty principle
That’s f’(x) over delta acceleration, not f(x)
Didn’t you read the answer from the pan dimensional white mice? The answer from Deep Thought was 42.
